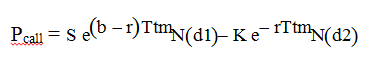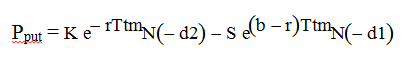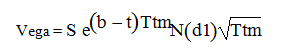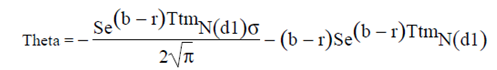Part II: End of day and online FX options pricing processes
This article is the continuation of the part I.
Each option contract can have its own pricing method. The implemented model is coded as for all OTC European FX option contracts set in DX.CONTRACT.MASTER:
This “GARMAN.KOHL” code is set in DX.PRICE.SOURCE table with following details:
Description:
DX.PR.BUILD.GK is the building program, which is firstly called by the pricing process.
DX.PR.GARMAN.KOHLHAGEN is the real pricing program, which is called with the following parameters:
INTSEQ = 51
VOLSEQ = 01
1.1 Pricing building program
The purpose of the “DX.PR.BUILD.GK” building program is to prepare the option pricing process by getting needed parameters.
Following parameters are initializing the common variable “C$DXPR.PRICE.RECORD” which is then transmitted to the pricing program using the“I_DX.PRICE.COMMON” library.
- Foreign currency and domestic currency are get from DX.CONTRACT.MASTER.
- Expiry date & remaining days are derived from the maturity date.
- Domestic and foreign interest rates are interpolated from PERIODIC.INTEREST using the curve key set in DX.PRICE.SOURCE field “5. CONS.DATA.NAME” = “INTSEQ” (example here “51”).
- Interest basis attached to the domestic currency
- Volatility of the currency pair is interpolated from DX.VOLATILITY using the curve key set in DX.PRICE.SOURCE field “5. CONS.DATA.NAME” = “VOLSEQ” (example “ 01”).
- FX spot rate for the currency pair is obtained using “CALL EXCHRATE”.
1.2 Pricing program
“DX.PR.GARMAN.KOHLHAGEN” program is computing a new price (replacement value) for each currency option in position.
Needed parameters are obtained by reading the common variable “C$DXPR.PRICE.RECORD” which is transmitted by the “I_DX.PRICE.COMMON” library.
1.2.1 Pricing step
The pricing step is using the market standard model used for FX options: Garman & Kohlhagen, which is an adaptation of the Black & Scholes model for FX European plain vanilla options. Compared to the initial model dedicated to interest rate options, the main adaptation consists in integrating a new “b = r – rf” variable, which is the difference of the risk-free rates attached to the two involved currencies .
Using the below parameters:
S= Spot price
K = strike
s = volatility
Ttm = time to maturity (e.g. days to maturity / basis)
R = domestic risk-free rate
Rf = foreign risk-free rate
b = r – rf
N(x) = Normal cumulative distribution of a probability “x”.
Note regarding Normal cumulative distribution approximations:
We can compute an accurate approximation using such a routine:
SUBROUTINE DX.CUMUL.NORM.DIST(VAR.IN, CND)
IN: VAR.IN= A random variable
OUT: CND= A probability that the random variable falls in the interval
[-infinite, VAR.IN]
========================================================================
a1 = 0.31938153
a2 = -0.356563782
a3 = 1.781477937
a4 = -1.821255978
a5 = 1.330274429
L = ABS(VAR.IN)
K1 = 1 / (1 + 0.2316419 * L)
CND = 1 - 1 / SQRT(2 * DX$PI) * EXP(-1*PWR(L,2) / 2) * (a1 * K1 + a2 * PWR(K1,2) + a3 * PWR(K1,3) + a4 * PWR(K1,4) + a5 * PWR(K1,5))
IF VAR.IN < 0 THEN
CND = 1 - CND
END
RETURN
END
Various figures are computed with this model, including prices and the greeks.
1.2.2 Call price
1.2.3 Put price
where
1.2.4 Delta
Delta is the option’s sensitivity to small movements in the underlying FX spot price.
For a call option:
D = e(b – Rd). T N(d1) (> 0)
For a put option:
D = e(b – Rd). T [N(d1)-1] (< 0)
1.2.5 Gamma
Gamma is the delta’s sensitivity to a small movement in the underlying FX spot price. Gamma is identical for put and call options.
1.2.6 Vega
Vega is the option’s sensitivity to a small movement in the volatility of the underlying currency pair. Vega is identical for put and call options.
1.2.7 Theta
Theta is the option’s sensitivity to a small change in time to maturity. As time to maturity decreases, it is normal to express the theta as minus the partial derivative with respect to time.
For a call option:
For a put option:
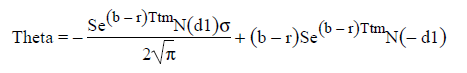
With N(-d1) = Normal distribution
To compute the required probability of such a Normal distribution, here’s an example of routine:
SUBROUTINE DX.NORM.DIST(INPUT.VALUE, SIGMA, MU, NORMAL.DIST) IN : INPUT.VALUE (the random variable, mandatory) SIGMA (optional) is the standard deviation, equals 1 when null. Note that SIGMA^2 = Variance. MU (optional) is the mean (e.g. an expectation), equals 0 when null OUT : NORMAL.DIST : a probability of standard normal distribution e.g. something between [0,1]. ============================================================================ IF (SIGMA = "") THEN SIGMA = 1 END IF (MU = '') THEN MU = 0 END NORMAL.DIST = 0 NORMAL.DIST = (1 / (SIGMA * SQRT(2 * DX$PI))) * EXP(-PWR((INPUT.VALUE-MU), 2) / 2*PWR(SIGMA,2)) RETURN END
1.2.8 Rho
Rho is the option’s sensitivity to a small change in the risk-free interest rate
1.2.9 Conversion step
The price given by the Black& Scholes model is expressed as forward pips.
This conversion step consists in transforming the forward pips into a rate format equivalent to each option’s open position. Because one cannot predict such format neiher the currency of the deal premium, we need to store equivalences in all formats, which is done using specific global variables:
P$DOM.PIPS: Price in PIPS en the domestic currency
P$FOR.PIPS: Price is PIPS in foreign currency
P$DOM.PRICE: Price in percentage in domestic currency
P$FOR.PRICE: Price in percentage in foreign currency
Following rules are applied, considering “GarmanKolhagen” as the replacement value expressed in forward pips returned by the pricing model:
First, check if one of the involved currency in a precious metal => FLAG.PREC.MET = 1
IF FLAG.PREC.MET = 0 THEN
P$DOM.PIPS = GarmanKolhagen * 10000
P$FOR.PRICE = GarmanKolhagen * 1/SPOT.PRICE * 100
P$DOM.PRICE = GarmanKolhagen / STRIKE.PRICE * 100
P$FOR.PIPS = GarmanKolhagen / (SPOT.PRICE * STRIKE.PRICE) * 10000
END ELSE
P$DOM.PIPS = GarmanKolhagen
P$FOR.PRICE = GarmanKolhagen * 1/SPOT.PRICE * 100
P$DOM.PRICE = GarmanKolhagen / STRIKE.PRICE * 100
P$FOR.PIPS = GarmanKolhagen / (SPOT.PRICE * STRIKE.PRICE)
END
1.3 End of day pricing process
In the batch DX.END.OF.DAY, the job DX.COB.PRICE.CHECK is launching the pricing process.
1.4 Online pricing process
Open FX options positions revaluation can either be done as part of the overnight batch utility or as an on-line process. This application allows the user to initiate an ad-hoc “what if” revaluation.
The DX.REVALUE application allows the entry of the selection criteria defining the trades/positions to be re-valued. Once the entries have been input and authorized the revaluation process passes control to the “Grey Box” processes (local pricing models).
The selection criteria is broken down into four sections, “who”, “by who”, “which trades”, and parameters.
• The “Who” consists of ALL.CUSTOMERS, GROUP, CUSTOMER and PORTFOLIO. If all customers are to be re-valued, the further “Who” selection fields are not available. For selection of individual Customers, Groups or Portfolios, set ALL.CUSTOMERS to “NO”. One can then identify a GROUP, CUSTOMER(s) or PORTFOILO(s). One can choose only one field to populate.
• The “By Who” section allows you to specify any number of DEALER.DESK(s)and/or DEPT.ACCT.OFFICER.
• The “Which Trades” allows the user to choose which kinds of trades from the customers selected to revalue. Either all, a particular CURRENCY, EXCHANGE, CONTRACT.CLASS or CONTRACT.
• The parameters allow the user to define which PRICE.SET is to be used during revaluation.
RE.CALCULATE.IM asks whether or not to calculate initial margin and is used to speed up the processing if only variation margin figures are needed. It is impossible to only calculate initial margin without running the variation margin routines, as initial margin often requires variation margin figures to be present.
RE.VALUE.LEVEL asks at which level the top-level summary information in DX.REVALUE.SUMMARY and DX.REVALUE.EXCHANGE is to be stored. This allows the system to calculate the total margins for either a PORFOLIO, a CUSTOMER, or a CUSTOMER group running An Ad-Hoc Revaluation
To set-up a revaluation, hit F3 to get the next available record id, and then define which customers/trades wish to be re-valued. Revaluation records cannot be re-used.
In order to start a revaluation process, the record must be input. The processing will begin when the record is authorized.
RE.CALCULATE.IM asks whether or not to calculate initial margin and is used to speed up the processing if only variation margin figures are needed. It is impossible to only calculate initial margin without running the variation margin routines, as initial margin often requires variation margin figures to be present.
RE.VALUE.LEVEL asks at which level the top-level summary information in DX.REVALUE.SUMMARY and DX.REVALUE.EXCHANGE is to be stored. This allows the system to calculate the total margins for either a PORFOLIO, a CUSTOMER, or a CUSTOMER group running An Ad-Hoc Revaluation
To set-up a revaluation, hit F3 to get the next available record id, and then define which customers/trades wish to be re-valued. Revaluation records cannot be re-used.
In order to start a revaluation process, the record must be input. The processing will begin when the record is authorized.
1.5 Prices storage
Once EOD or online pricing has been triggered, results are stored in the standard file DX.MARKET.PRICE.
Keys of this table, which are created everytime a new deal is opening a new position with empty data is structured like this:
- Price set (closing / Intraday)
- FX currency pair (e.g. contract code from DX.CONTRACT.MASTER)
- Premium currency
- Maturity date
- Call / Put
- Strike price
Example: for a Call USD/EUR strike 1.33 maturing on 25/03/2013: